… by utilizing Deleuzoguattarian philosophy

Zeno of Elea, a prominent Greek philosopher and mathematician, posited a series of paradoxes aimed at critically examining the concepts of space and time. Among Zeno’s paradoxes, the one I particularly favor is Zeno’s Dichotomy — simply referred to as Zeno’s Paradox. This paradox is concerned with the infinite divisibility of space.

To begin, Achilles (a literary Greek hero) starts at the beginning of a racetrack. As with all races, the goal is to go from the starting point (point A) to the finish line (point B). A simple illustration maps the racetrack Achilles is on:

A — — — — — — — — — — — — — — — — B

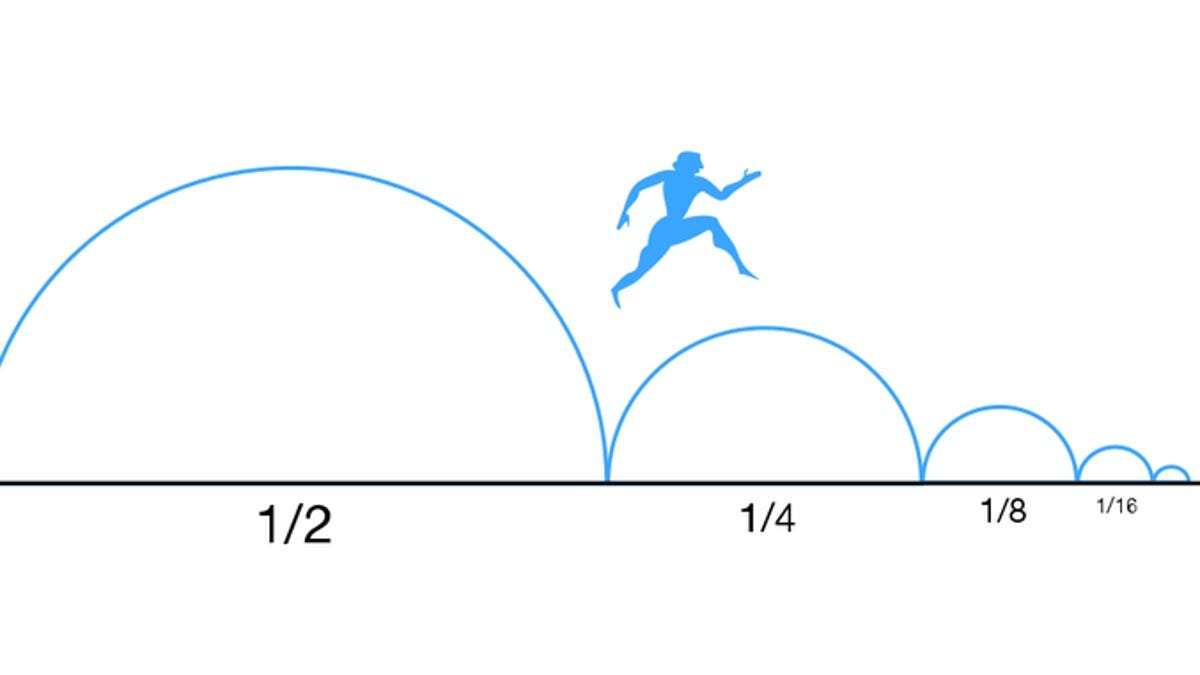
This paradox details the constant multiplication of Achilles’ spatial point by 1/2 after he reaches the halfway point between A and B (we will call this halfway point ‘A1’). Once Achilles reaches A1, he must now reach the halfway point between A1 and B; thus, he must reach A2. As seen in Figure One, this process repeats ad infinitum as Achilles’ distance traveled is repeated to the ‘nth’ degree.

Each time Achilles reaches a halfway point, there will always be another halfway point between the point he is on and B — no matter how small the distance. If Achilles were in a one-mile race (with “m” representing “miles”), he would need to cross an infinite number of points. The paradox goes as follows:

A1 = 1/2m

A2 = 1/4m

A3 = 1/8m

A4 = 1/16m

… ad infinitum …

Because of this paradox, Zeno held the belief that motion was illusory. Simply put, Zeno accepted the premises and conclusions of his own argument leading him to believe that motion is like that of a hallucinatory experience.

Let’s isolate the logic behind the paradox:

1. Premise one: In order to travel from point A to point B, a traveler must traverse an infinite number of points (and these points must have a length greater than zero).
2. Premise two: A traveler cannot traverse an infinite number of points.
3. Conclusion: Motion cannot exist as a traveler cannot traverse an infinite number of points.

This is a paradox as the logic offers a valid argument with seemingly true premises and a seemingly true conclusion (albeit unacceptable).

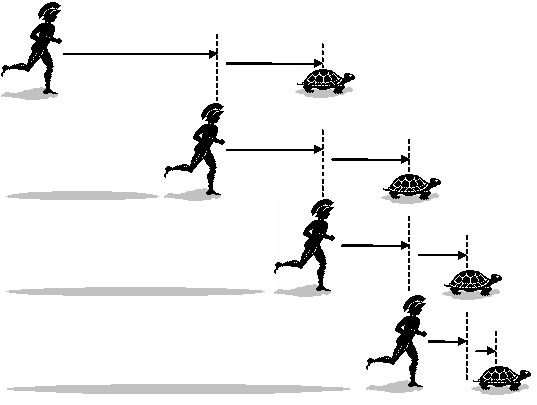
Note: Sometimes this paradox is explained through Achilles and the tortoise.

What are our options here?

Firstly, one can simply accept the conclusion. For us to accept this conclusion, we would have to adhere to the idea that motion is impossible and our reality experienced is an illusion. For me, there is a level of difficulty in believing that each of our realities are that of an illusion or hallucination.

Secondly, one can discredit the validity of the argument presented. This (along with the first option) does not suffice as classical logic entails the validity of Zeno’s argument.

What constitutes a valid argument?

A valid argument can be conceptualized through the form:

1. For all x, if x is C, then x is D.

2. No x is C.

3. Therefore, no x is D.

In the context of the form above, let us assume for a moment that:

C = Travels from point A to point B

D = Traverses an infinity of intervals (with a sum greater than zero)=

For a valid argument to exist, there must exist a valid form. A valid argument can never result in a situation where an argument has true premises and a false conclusion, so if the paradox has a valid form, then that indicates the argument is valid. C, in this form, equates to ‘travels from point A to point B’; and we have the statement: If x is C, then x is D. This indicates that if one were to travel from point A to point B (C), then that must indicate that one would have to traverse an infinity of intervals of non-zero length (D). Thus, the argument is valid.

3. Thirdly, one can question one or both premises presented in the paradox.

The first premise isolates that there are an infinite number of points in a line. Premise one deniers offer a compelling claim that elucidates the idea that a finite segment cannot contain an infinite number of points. They argue that the sum of each point between A and B would be infinity. Therefore, because the A-B segment itself is not infinite, there cannot be an infinite number of points between A and B.

Premise one, however, should be deemed legitimate. A track can continue to be divided in half as Achilles’ spatial point consistently multiplies by ½. For Achilles at A1 to reach B, he needs to reach A2 (the halfway point between A1 and B). And for Achilles at A2 to reach B, he needs to reach A3 (the halfway point between A2 and B). This process continues ad infinitum. Thus, if we conclude that premise one is true, and we believe the conclusion to be false, then we can presume that premise two is invalid.

**It’s important to note that premise one deniers lack a logical explanation for why a line cannot continue to be divided in half. At what point can we no longer divide in half?

The second premise isolates that a traveler cannot traverse an infinite number of points. To prove that premise two is invalid, it is necessary to bring in the concept of standard limit analysis into this paradox. As we are aware, the A-B segment is a finite segment divided into parts; and we can measure the lengths of each spatial point in relation to each other. For example, if the length between A and B is a mile, then the length between A1 and B is 1/2 of a mile. The length between A2 and B is 1/4 of a mile. The length between A3 and B is 1/8 of a mile … ad infinitum.

However, as the length between Achilles’ spatial point and B decrease (as Achilles continues with the race), Achilles would have to traverse the length of these points:

1/2m + 1/4m + 1/8m + 1/16m + 1/32m + 1/64m + … 1/(2^n)m

*m = mile

In calculus, we have a standard limit analysis that is composed of infinite series which allows us to examine the addition of an infinite series of numbers. Here is an equation which proves this:

Thus, under this standard analysis, we can add each partial sum and note the added spatial points converging to one:

1/2m

1/2m + 1/4m = 3/4m

1/2m + 1/4m + 1/8m = 7/8m

1/2m + 1/4m + 1/8m + 1/16m = 15/16m

… …

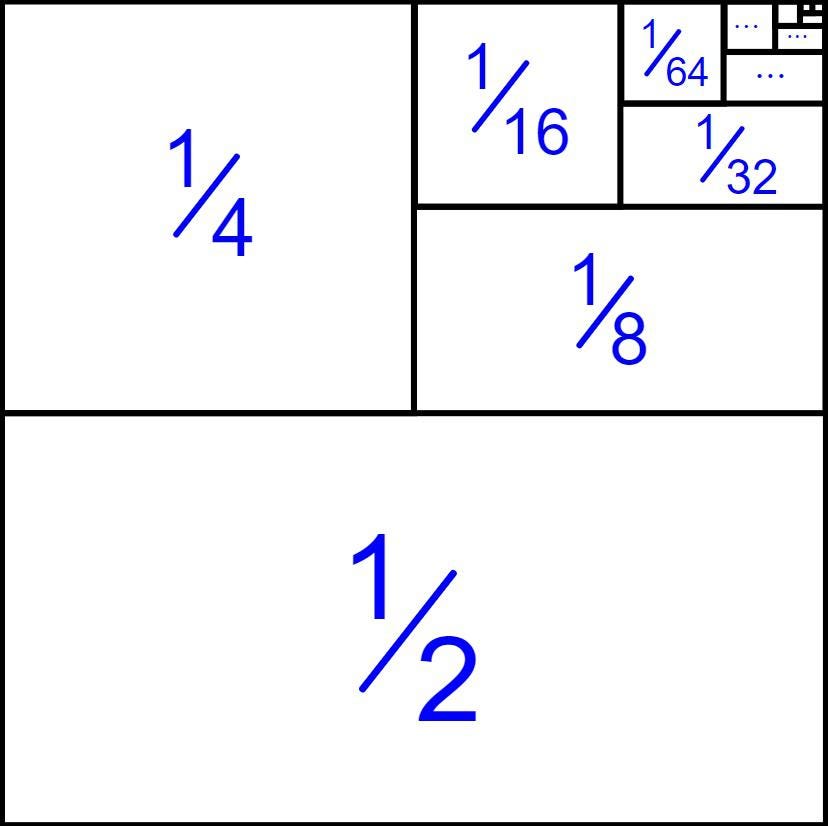
When we add the total number of lengths that Achilles’ crosses, the total sum should converge to 1 (in this example, it would specifically converge to one mile). There is a fantastic visual depiction of this where we can isolate a square being divided an infinite number of times, but the square still equates to one (a single square). This is seen in Figure Five.

While the rejection of premise two is highly compelling for some, we should challenge this notion by introducing the concept of supertasks.

What is a supertask?

A supertask is an operation dealing with a countable infinity sequence that sequentially occurs over a finite amount of time.

As the completion of a supertask is incoherent, there is a valid argument to be made that discards the argument against premise two. In the context of this paradox, a valid criticism regarding the impossibility of supertasks lies within Thomson’s lamp. Imagine a lamp that is turned off exactly at 11:59 PM. After 1/2 of a minute, the lamp is turned on. After 1/4 of a minute, the lamp is turned off. After 1/8 of a minute, the lamp is turned on … ad infinitum. What is the state of the lamp after one minute?

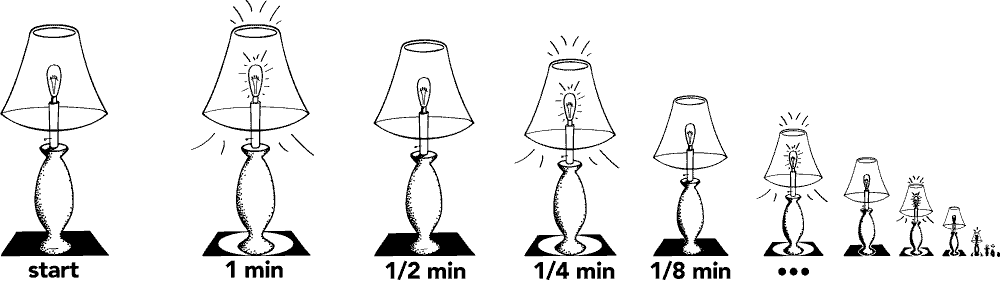
If the lamp is off at the end of the supertask, there should have been a moment where the lamp was turned on. If the lamp is on at the end of the supertask, there should have been a moment where the lamp was turned off. The idea that we cannot complete a supertask upholds premise two of Zeno’s dichotomy — one cannot complete an infinite number of tasks.

Yet, the completion of the supertask assumes it can be started in the first place.

Let’s reverse this with Bernardete’s Paradox

This entire time, we have been theorizing Achilles having the ability to leave point A in order to reach A1. In fact, we’ve also theorized (in Thomson’s lamp), that 30 seconds is able to pass.

But, if we reverse Zeno’s Dichotomy, we will find that Achilles should not be able to reach A1 as there are an infinite number of points between point A and A1. And for Achilles to raise his hand for one second on A1, that would require 30 seconds to pass. However, 30 seconds should not be able to pass without 15 seconds passing first. And 15 seconds should not be able to pass without 7.5 seconds passing first … ad infinitum …

Bernardete’s Paradox is best described through this blog post. Essentially, imagine an individual walking towards a point. This individual will continue walking past point A unless something stops this individual.

In this paradox, there are an infinite number of gods who will create a barrier stopping this individual from furthering their distance if the individual reaches a certain point.

According to the blog above:

(1) G1 will erect a barrier at exactly ½ meter past A if Alice reaches that point.

(2) G2 will erect a barrier at exactly ¼ meter past A if Alice reaches that point.

(3) G3 will erect a barrier at exactly 1/8 meter past A if Alice reaches that point.

And so on.

Note that the possible barriers get arbitrarily close to A. Now, what happens when Alice approaches A?

Alice’s forward progress will be mysteriously halted at A, but no barriers will have been erected by any of the gods, and so there is no explanation for Alice’s inability to move forward.

Proof: Imagine that Alice did travel past A. Then she would have had to go some finite distance past A. But, for any such distance, there is a god far enough along in the list who would have thrown up a barrier before Alice reached that point. So Alice can’t reach that point after all. Thus, Alice has to halt at A. But, since Alice doesn’t travel past A, none of the gods actually do anything.

This is similar to Zeno’s Dichotomy. Though the purpose of this blog is not about Bernardete’s Paradox, it is still important to conceptualize Zeno’s implications of movement.

Let’s look at this temporally

Examining Zeno’s Paradox in a staccato format, specifically the time Achilles takes to reach point B, reveals a challenge in resolving the paradox, particularly within the context of supertasks.

Instead of Achilles solely traversing the points on the track, we will now require him to raise his hand for one second at each interval he reaches while also dividing the time it takes for him to reach each interval (by ½). For example, from A to A1, Achilles takes half a minute, raising his hand for one second at A1. Then, from A1 to A2, it takes him a quarter of a minute, followed by another one-second hand raise at A2. This iterative process persists indefinitely.

While the points on the racetrack converge to one, each second dedicated to Achilles raising his hand introduces a challenge wherein Achilles seemingly never reaches the finish line due to the infinite time it would take. However, the issue doesn’t lie in completing an infinite number of actions; instead, it centers on Achilles consistently raising his hand for the same duration at each interval.

However, let us now argue that we can equate the time it takes for Achilles to reach each interval with the amount of time it takes to raise his hand (with a one-to-one correspondence). For example, from A to A1 Achilles takes half a minute and at A1 he raises his hand for half a second. From A1 to A2 it takes Achilles a quarter of a minute, and at A2 he raises his hand for a quarter of a second. As this process continues, it would entail the time of the traversal of intervals converging to one minute and the time of the hand raising converging to one second.

However, let’s posit that we can establish an equivalence between the time Achilles takes to reach each interval and the duration of raising his hand (maintaining a one-to-one correspondence). For instance, from A to A1, Achilles takes half a minute, and at A1, he raises his hand for half a second. Subsequently, from A1 to A2, Achilles takes a quarter of a minute, raising his hand for a quarter of a second at A2. This ongoing process would lead to the time for traversing intervals converging to one minute, while the time for raising the hand converges to one second. Thus, Achilles would take one minute and one second to reach point B.

However, there’s a crucial assumption here — the assumption that time is capable of passing. To attain one minute, we must first reach A1 (30 seconds), then A2 (45 seconds), and so on, ad infinitum. Conversely, we can reverse this process; to reach 30 seconds, we initially need to reach 15 seconds, and so forth.

Therefore, by applying Zeno’s Paradox to temporality, time itself is not able to pass.

So, here we are. Stuck. Without motion. Without the passage of time.

Therefore, we must formulate a spatiotemporal ontology that extends beyond the existing limitations.