… by utilizing Deleuzoguattarian philosophy
This blog post aims to provide a solution to Zeno’s Paradox. The first blog post on this topic can be accessed here.
**Citation Note: Full citation provided at the end of this post
Gilles Deleuze and Félix Guattari’s collaborative work, A Thousand Plateaus, introduces the concepts of smooth and striated space. In the plateau titled The Smooth and the Striated, Deleuze and Guattari embark upon an exploration of spatialization that challenge current, normative limitations of space.
They begin their section titled The Mathematical Model by praising Bernhard Riemann for his discovery of the multiplicity:
It was a decisive event when the mathematician Riemann uprooted the multiple from its predicate state and made it a noun, “multiplicity.”
It marked the end of dialectics and the beginning of a typology and topology of multiplicities.
(ATP, 482–483)
Traditionally, mathematics has been framed by assessing mathematical entities in comparison to other mathematical entities, like evaluating the magnitudes of two different lines. Deleuze and Guattari isolate Riemann’s transformative shift in mathematics as he departs from the traditional, predicate state in which math is typically viewed. Riemann establishes a new paradigm where each mathematical entity is not exclusively defined in relation to other mathematical entities, but is characterized by a multitude of intrinsic characteristics within itself. As Deleuze and Guattari express, “each multiplicity was defined by n determinations; sometimes the determinations were independent of the situation, and sometimes they depended on it” (ATP, 483).

So … what does it mean for the determinations of a multiplicity to be independent or dependent of the situation?
Thankfully, Deleuze and Guattari give two examples which will help us delineate the differentiation between a multiplicity whose determinations are independent of the situation and a multiplicity whose determinations depend on the situation.
The first example is the comparison between two lines: “the magnitude of a vertical line between two points can be compared to the magnitude of a horizontal line between two other points … its determinations are magnitudes” (ATP, 483; emphasis mine). In this scenario, when comparing the magnitudes of these distinct lines, their determinations are independent of the situation. This independence stems from the fact that the comparison between these lines can occur without specific reference to a broader context, indicating that the determinations of magnitude are not reliant on the specific situation.
An illustration of this concept is evident in Figures Three and Four, where the comparison between the two lines is not inherently tied to specific spatial details but is instead based on their lengths, which, notably, do not depend on any specific spatial considerations (making it a generalizable concept that holds true across various settings).
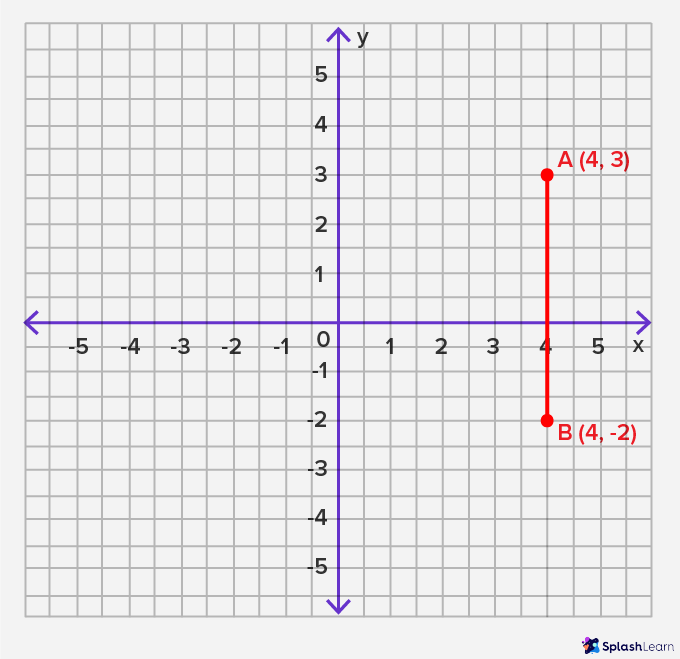
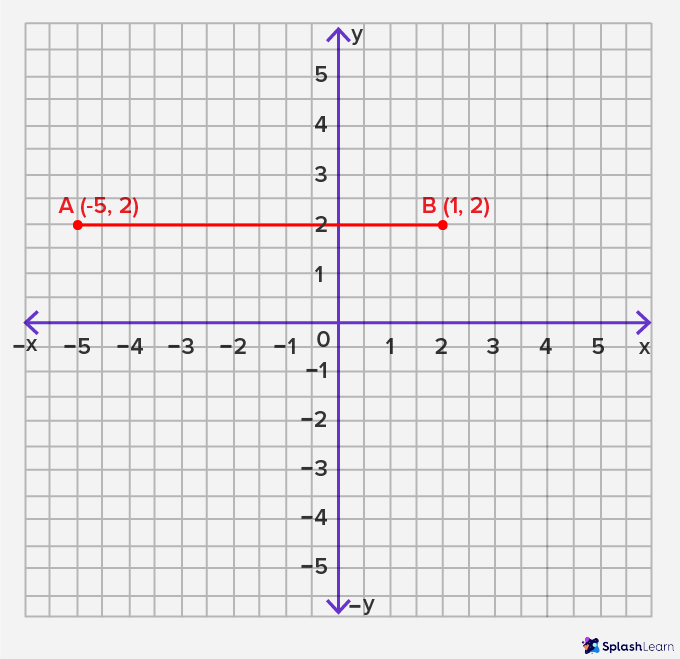
In this first example, “it is clear that the multiplicity […] is metric, that it allows itself to be striated, and that its determinations are magnitudes” (ATP, 483; emphasis mine).
The concept of striated space directly contrasts the subsequent example, where Deleuze and Guattari emphasize a scenario where the determinations of multiplicities are contingent on the specific situation. As illustrated in their second example, “two sounds of equal pitch and different intensity cannot be compared to two sounds of equal intensity and different pitch” (ATP, 483; emphasis mine). In this instance, a universally applicable method for comparing these two sounds is absent. While one might endeavor to make such a comparison between “two sounds of equal pitch and different intensity” and “two sounds of equal intensity and different pitch”, the task is quite difficult.
In the context of sound comparison, Deleuze and Guattari state that:
Two determinations can be compared only ‘if one is a part of the other and if we restrict ourselves to the judgment that the latter is smaller than the former, without being able to say by how much.’” (ATP, 483)
This statement suggests that the comparison between “two sounds of equal pitch and different intensity” and “two sounds of equal intensity and different pitch” relies on a restricted, delimited, and particular judgement. Such a comparison necessitates a shared quality between the two sounds that can be assessed, coupled with the ability to discern which sound is smaller or larger. Notably, this comparison lacks a numerical or quantitative measure to specify an exact degree of difference — it is purely a relative judgement.
Deleuze and Guattari state:
Multiplicities of this second kind are not metric and allow themselves to be striated and measured only by indirect means, which they will always resist.
They are anexact yet rigorous.
(ATP, 483; emphasis mine)
Multiplicities of this second kind allow themselves to be smoothed.
Prior to delving into Zeno’s Paradox, we must first analyze the difference(s) between distance and magnitude.
Distance vs. Magnitude
Following Deleuze and Guattari’s examination of striation and smoothness in space, they delve into an examination of the distinctions between distance and magnitude.
They write:
Distances are not, strictly speaking, indivisible: they can be divided precisely in cases where the situation of one determination makes it part of another. But unlike magnitudes, they cannot divide without changing in nature each time.
(ATP, 483; emphasis mine)
To articulate their argument, Deleuze and Guattari provide examples of intensities, like distance, changing in nature with each division. They emphasize that intensities are not “composed of addable and displaceable magnitudes” (ATP, 483). This assertion is illustrated through two specific examples: temperature and speed. When we conceptualize temperature and speed as intensities, it is quite obvious that “a temperature is not the sum of two smaller temperatures” and that “a speed is not the sum of two smaller speeds” (ATP, 483). This concept applies to distance as an intensity because a distance is not the sum of two smaller magnitudes; rather, it undergoes a change in nature with each division.
Deleuze and Guattari state:
Since each intensity is itself a difference, it divides according to an order in which each term of the division differs in nature from the others.
(ATP, 483)
So … what exactly is distance?
Distance is therefore a set of ordered differences, in other words, differences that are enveloped in one another in such a way that it is possible to judge which is larger or smaller, but not their exact magnitudes. (ATP, 483; emphasis mine)
To elucidate this point further, let us utilize an example of a straight line segment AB in a geometric space:

In this scenario, the divisibility of distance becomes apparent. Of course we are able to divide the AB segment into smaller segments. Notably, distinct halfway points exist between A and B (designated as ‘A1’); and similar halfway points persist in subsequent divisions (A2, A3, etc.). As previously mentioned, the comparison of lines in a metric fashion is feasible because the line’s determinations are its magnitudes. The magnitude of a line, reflecting its overall length or size, may alter if the line is extended or shortened, but the inherent nature of a line’s determinations being magnitudes remains constant — this is an example of the striation of space. On the other hand, when considering the distance of a line — measuring specific points or segments — each division alters the localized nature of those distances, reshaping the line in those specific contexts — this is an example of the smoothness of space. The magnitude encompasses the line as a whole, while distance focuses on the specific measurements between points, and changes in these distances bring about shifts in the line’s characteristics at those particular instances.
Although one can quantify the distance of the AB segment, distance is analogous to what we observed with temperature and speed. It is crucial to note that, akin to temperature and speed, a line’s distance is not comprised of addable and displaceable magnitudes.
Let us use another one of Deleuze and Guattari’s example:
One can divide movement into the gallop, trot, and walk, but in such a way that what is divided changes in nature at each moment of the division, without any one of these moments entering into the composition of any other. (ATP, 483)

In this case, there is a fundamental qualitative change over the course of a horse’s movement. This YouTube video by Dave Harris gives a fantastic explanation of this very movement:
The motion of a horse also involves qualitative change — as it gets faster, it’s not just a quantitative increase in velocity that we observe, but a qualitative change from walk to trot to cantor to gallop.
To sum up this portion dedicated to delineating the difference between distance and magnitude, Deleuze and Guattari write:
Therefore these multiplicities of “distance” are inseparable from a process of continuous variation, whereas multiplicities of “magnitude” distribute constants and variables.
(ATP, 483; emphasis mine)
Bergson, Riemann, and Duration
It is not just Riemann that Deleuze and Guattari praise, but also Henri Bergson. In Bergson’s 1889 work, Time and Free Will, “he presents duration as a type of multiplicity opposed to a metric multiplicity or the multiplicity of magnitude” (ATP, 483; emphasis mine).
**Note because I got confused here: “metric multiplicity” and “multiplicity of magnitude” are the same. Deleuze and Guattari use the word “or” to denote that these are synonymous terms.
**According to a quick Google search, duration is “the time during which something continues” (Oxford Languages).

Much like distance, “Duration is in no way indivisible, but is that which cannot be divided without changing in nature at each division” (ATP, 483). And, as previously mentioned, duration does not belong to the realm of metric multiplicity (the multiplicity of magnitude). In this context, Deleuze and Guattari introduce the concept of homogeneous extension, isolating that magnitude falls within this category (and that duration does not fall within this category):
In a multiplicity such as homogeneous extension, the division can be carried as far as one likes without changing anything in the constant object; or the magnitudes can vary with no other result than an increase or a decrease in the amount of space they striate. (ATP, 483–484)
Let’s examine the two components of homogeneous extension:
- “The division can be carried as far as one likes without changing anything in the constant object.” This refers to the nature of magnitudes. It suggests that a constant object, which is associated with magnitudes, can be continually divided into smaller parts without undergoing any alterations in its inherent properties or characteristics because the magnitudes stay the same. The emphasis lies in the object’s divisibility, conveying the idea that it can be subdivided endlessly while preserving its fundamental attributes.
- “The magnitudes can vary with no other result than an increase or a decrease in the amount of space they striate.” This refers to the variations in the length of the constant object, signifying the magnitude’s capacity to undergo changes in its spatial extent. However, this does not entail magnitude changing its nature. Whether the magnitude increases or decreases, the alteration occurs within the realm of the space it occupies or striates.
The crucial distinction lies in the continuous nature of duration, in contrast to homogeneous extension where space is striated. Magnitude shares characteristics of homogeneous extension, but duration remains distinct due to its continuous and transformative nature with each division.
Therefore, “Bergson thus brought to light ‘two very different kinds of multiplicity,’ one qualitative and fusional, continuous, the other numerical and homogeneous, discrete” (ATP, 484). Duration represents a qualitative and fusional multiplicity, setting it apart from numerical and homogeneous multiplicities.
Note: Deleuze and Guattari briefly mention that “matter goes back and forth between [the two very different kinds of multiplicity]” while referencing the contentious debate between Bergson and Einstein.

Major Science vs. Minor Science
To sum up thus far:
We have on numerous occasions encountered all kinds of differences between two types of multiplicities: metric and nonmetric; extensive and qualitative; centered and acentered; arborescent and rhizomatic; numerical and flat; dimensional and directional; of masses and of packs; of magnitude and of distance; of breaks and of frequency; striated and smooth.
(ATP, 484; emphasis mine)
Deleuze and Guattari further emphasize that multiplicities that change their nature with every division occupy a smooth space; they give the example of “tribes in the desert” (ATP, 484). The tribe serves as an example of a multiplicity that changes in nature with each division and the desert itself serves as a smooth space.

At any rate, given that mathematics primarily involves numbers, one might presume that “the Number would belong exclusively to the other multiplicities,” particularly those of the metric (ATP, 484). Deleuze and Guattari express a partial agreement with this notion:
It is true that the number is the correlate of the metric: magnitudes can striate space only by reference to numbers, and conversely, numbers are used to express increasingly complex relations between magnitudes, thus giving rise to ideal spaces reinforcing the striation and making it coextensive with all of matter. (ATP, 484)
This is evident in the “correlation within metric multiplicities between geometry and arithmetic, geometry and algebra, which is constitutive of major science” (ATP, 484). In smooth space, the emphasis is on qualitative characteristics, with inherent limitations on calculations. However, Deleuze and Guattari challenge the perceived ‘inferiority’ of smooth space:
For the independence of this nearly illiterate, ametric geometry is what makes possible the independence of the number, the subsequent function of which is to measure magnitudes in striated space (or to striate).
The number distributes itself in smooth space; it does not divide without changing nature each time, without changing units, each of which represents a distance and not a magnitude.
(ATP, 484–485)
They end this paragraph by articulating how minor science contributes to major science:
Minor science is continually enriching major science, communicating its intuitions to it, its way of proceeding, its itinerancy, its sense of and taste for matter, singularity, variation, intuitionist geometry and the numbering number. (ATP, 485)
Quick Note — There are two aspects of smooth space …
… But so far, we have only gone over the first aspect of smooth space:
The situation of one determination can make it part of another without our being able either to assign that situation an exact magnitude or common unit, or to discount it. (ATP, 485)
Distance, for example, is a set of ordered differences distinct from that of magnitude — distances do not consist of magnitudes that can be added or displaced. The first aspect of smooth space isolates that a smooth multiplicity populates a smooth space in the same manner that distance populates smooth space.
The second aspect of smooth space is:
When the situation of the two determinations precludes their comparison. (ATP, 485)
We will be going over this second space now.
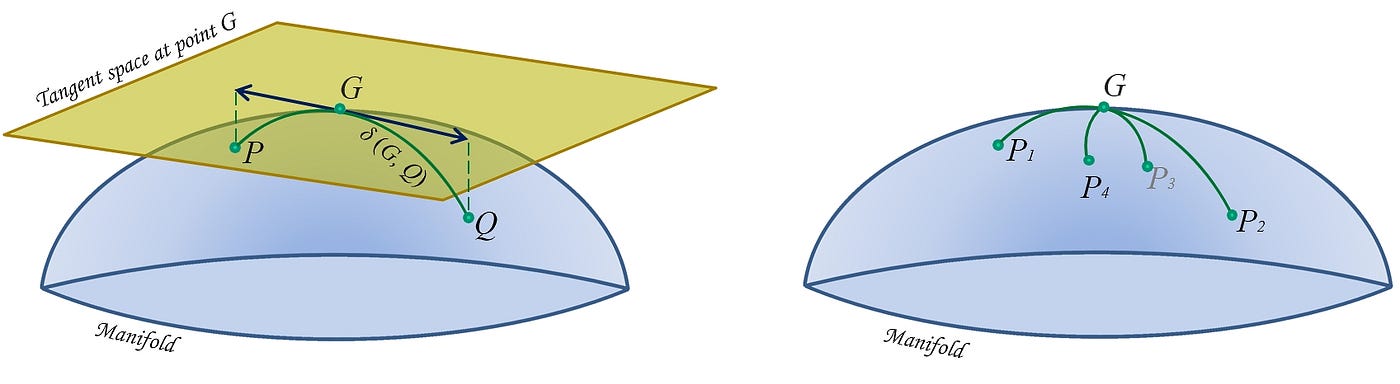
Euclidean Space vs. Riemannian Space
Instead of conceptualizing space as entirely flat, and easily measureable — Deleuze and Guattari introduce the concept of smooth, Riemannian spaces. Riemannian spaces can exhibit positive, negative, or zero curvature. For instance, two parallel lines on a flat, Euclidean space never meet, but in a Riemannian space, they might — or at least the parallel lines have the potentiality to meet.
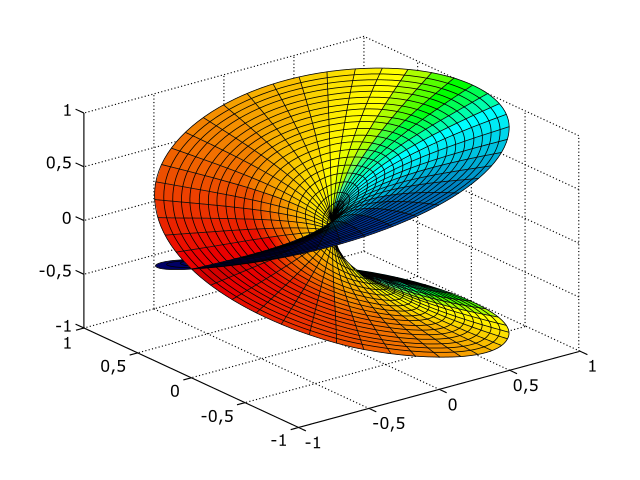
Deleuze and Guattari cite someone (I can not find exactly who) that provides a vivid illustration of observers in a Riemannian space:
“It follows that two neighboring observers in a Riemann space can locate the points in their immediate vicinity but cannot locate their spaces in relation to each other without a new convention. Each vicinity is therefore like a shred of Euclidean space, but the linkage between one vicinity and the next is not defined and can be effected in an infinite number of ways. Riemann space at its most general thus presents itself as an amorphous collection of pieces that are juxtaposed but not attached to each other.”
(ATP, 485)
According to Deleuze and Guattari, defining observers in relation to one another in a Riemannian space can be achieved without relying on a metrical, Euclidean system. They suggest that this measurability is accomplished “in terms of the conditions of frequency, or rather accumulation, of a set of vicinities” (ATP, 485). This process resembles an earlier example of comparing sounds, demonstrating an “anexact, yet rigourous” measurement of observers in a Riemannian space. This represents the second aspect of smooth space: “When, independent of metrics, determinations arise that cannot be part of one another but are connected by processes of frequency or accumulation” (ATP, 485).
Nevertheless, Deleuze and Guattari acknowledge that the metric measurability of these observers “necessarily results” from processes of frequency and accumulation. Let’s illustrate with an example of how Euclidean space imposes striation on the smooth space of Riemann.
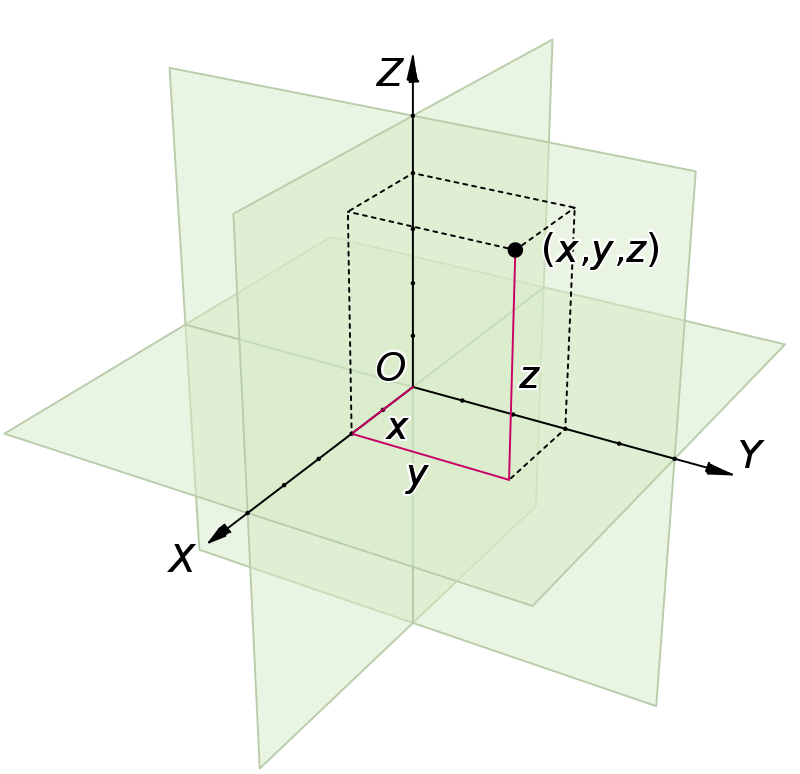
Deleuze and Guattari contend that normative perspectives of space depict space as purely flat or striated. This is seen in classical Euclidean geometry which examines points on a line in relation to other points. As seen in Figure Two, Euclidean space is striated in any dimension it operates on. In a 2-Dimensional plane, coordinates are represented through x and y; in a 3-Dimensional plane, the coordinates are represented through x, y, and z. Euclidean geometry’s scope is not confined to two or three dimensions; it extends into higher dimensions as represented by x1, x2, x3, x4, x5 … xn.
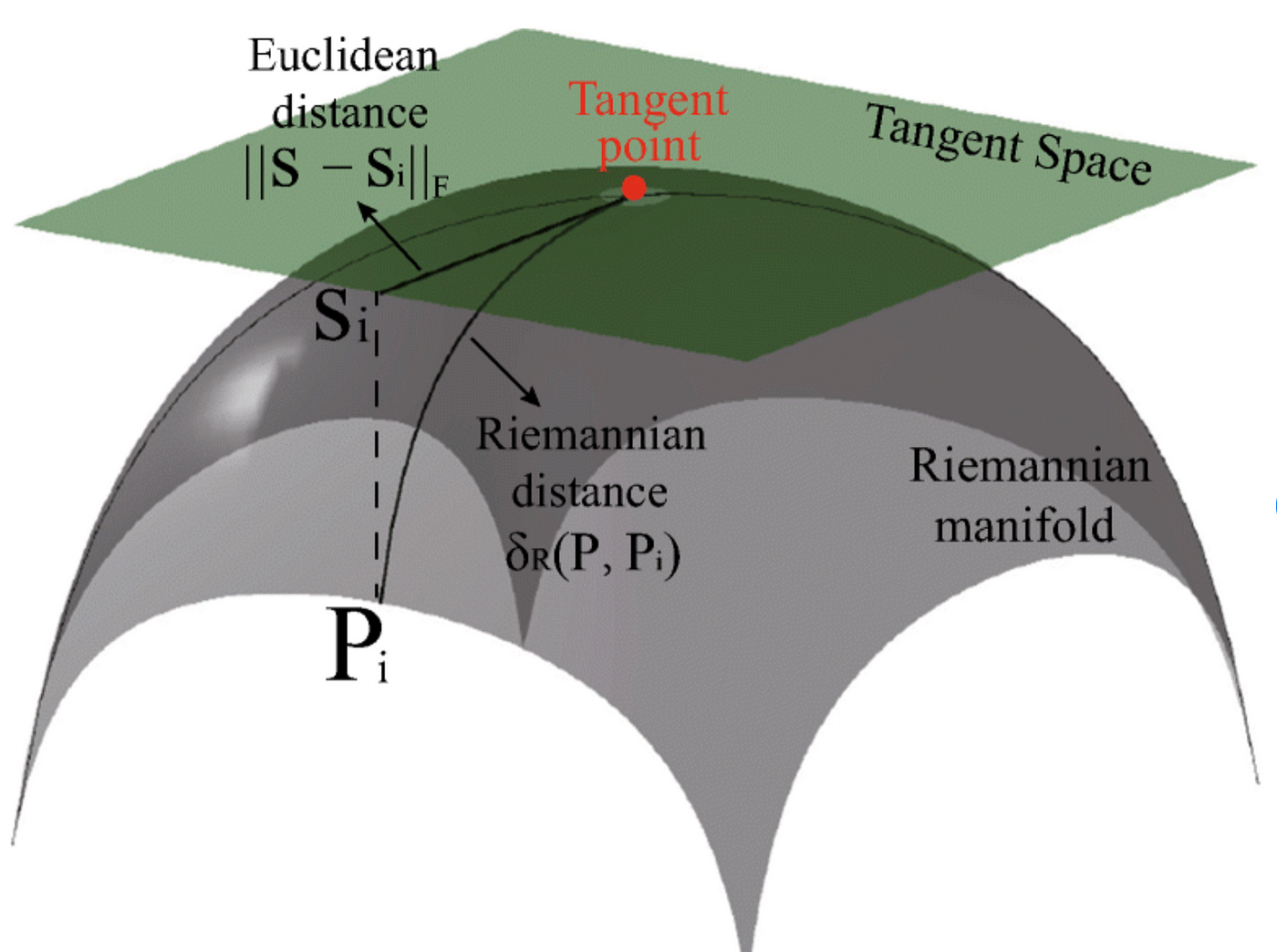
Observe in Figures Thirteen and Fourteen the grid-like striation of the Riemannian (hemi-)sphere/manifold. Here, Euclidean space imposes its striating influence on the smooth Riemannian space through the introduction of tangent planes. Euclidean space needs to localize specific points in a narrow manner. The introduction of tangent planes in relation to Riemannian spaces are necessary to introduce a quantitative, structured order and measurement upon the fluid Riemannian space.
Deleuze and Guattari write:
We are always brought back to a dissymmetrical necessity to cross from the smooth to the striated, and from the striated to the smooth.
(ATP, 486)
This process of smooth → striated and striated → smooth occurs through the process of translation.
[Translation] is an operation that undoubtedly consists in subjugating, overcoding, metricizing smooth space, in neutralizing it, but also in giving it a milieu of propagation, extension, refraction, renewal, and impulse without which it would perhaps die of its own accord: like a mask without which it could neither breathe nor find a general form of expression. (ATP, 486)
Deleuze and Guattari give two examples of translations that provide “opportunities for openings [and] risks of closure or stoppage” (ATP, 486).
- The first example of translation deals with translating intensities into extensive quantities.
This resembles the transformation of a “multiplicity of distance into systems of magnitudes,” where the systems of magnitudes impose striations on the multiplicities of distance (ATP, 486). Consider the temperature example mentioned earlier: in a smooth space, temperature is perceived through a range of qualitative sensations. Yet, we have the ability to convert these intensities into a structured system of magnitudes.
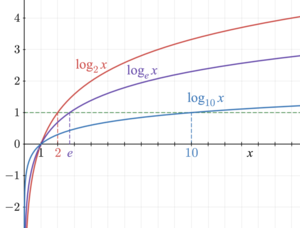
- *Deleuze and Guattari illustrate the first type of translation with the example of a logarithmic function. A logarithm serves as an inverse operation of exponentiation. Khan Academy has a wonderful video detailing what a logarithmic function is.
2. The second example of translation is “the means by which Riemannian patches of smooth space receive a Euclidean conjunction” (which was explained previously) (ATP, 486).
- *Deleuze and Guattari illustrate the second type of translation with the example of the “parallelism of vectors in striating the infinitesimal” (ATP, 486). The parallelism of vectors determines the maintenance of a consistent, coherent direction between vectors; this imposes order to the infinitesimally small points within Riemannian space.
Nothing is ever done with: smooth space allows itself to be striated, and striated space reimparts a smooth space, with potentially very different values, scope, and signs.
Perhaps we must say that all progress is made by and in striated space, but all becoming occurs in smooth space.
(ATP, 486)
Fractals and Sponges
To come up with a generalizable, mathematical definition of a smooth space, Deleuze and Guattari refer to mathematician Benoit Mandelbrot’s “fractals”. Deleuze and Guattari write:
Fractals are aggregates whose number of dimensions is fractional rather than whole, or else whole but with continuous variation in direction. (ATP, 486)

An eloquent and vivid manner to portray a fractal can be found in Deleuze and Guattari’s depiction of Van Koch’s Curve.
An example [as shown in Figure Eighteen] would be a line segment whose central third is replaced by the angle of an equilateral triangle; the operation is repeated for the four resulting segments, and so on ad infinitum, following a relation of similarity — such a segment would constitute an infinite line or curve with a dimension greater than one, but less than a surface (= 2). (ATP, 486)
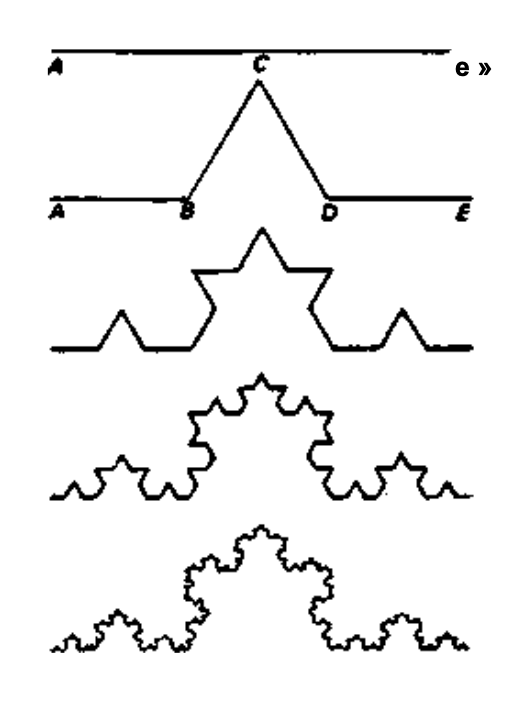
In Figure Eighteen, we encounter a phenomenon described as “more than a line” but “less than a surface” (ATP, 487). Van Koch’s Curve concludes this phenomenon, presenting a structure comprising “an infinite number of angled points that prevent any tangent from being drawn to them” (ATP, 487).” This resistance of smooth space to organizational efforts is evident; the very act of preventing tangents on the line serves as an example of smooth space resisting striation. In the YouTube video, Deleuze for the Desperate #9: smooth space, Dave Harris highlights that “the length of a fractal line cannot be definitively established because it continuously branches off to enclose additional shapes.”
Attempts by Euclidean geometry to structure a fractal necessitate the localization of a portion for measurement, revealing the inherent limitation of this method. Functioning as a form of striation, Euclidean geometry is unable to engage with the fractal as a whole with fractional dimensions. Instead, it is confined to a specific line or area, limiting its capacity to grasp the intricate complexity of the entire fractal structure. Viewed through a Euclidean lens that considers points as fixed, a distant analysis of a fractal (i.e., observing it from a distance) might simplify its intricate details into what appear to be straightforward lines or curves. Nevertheless, as we zoom into the fractal, more dimensions emerge.
Harris states:
As a result, they are not just normal straight lines with a straightforward connection between two points — that would have a dimension of 1 … But they don’t exactly occupy a regular surface either — a 2D flat space. It can only be represented by a fraction or decimal between 1 and 2.
Another example of a smooth space is that of the Sierpinksi Sponge (sometimes referred to as the ‘Menger Sponge’) as seen in Figure 19. Deleuze and Guattari write:
Each square hole is surrounded by eight holes a third its size.
These holes are in turn surrounded by eight holes, also a third their size.
And so on, endlessly.
(ATP, 487)
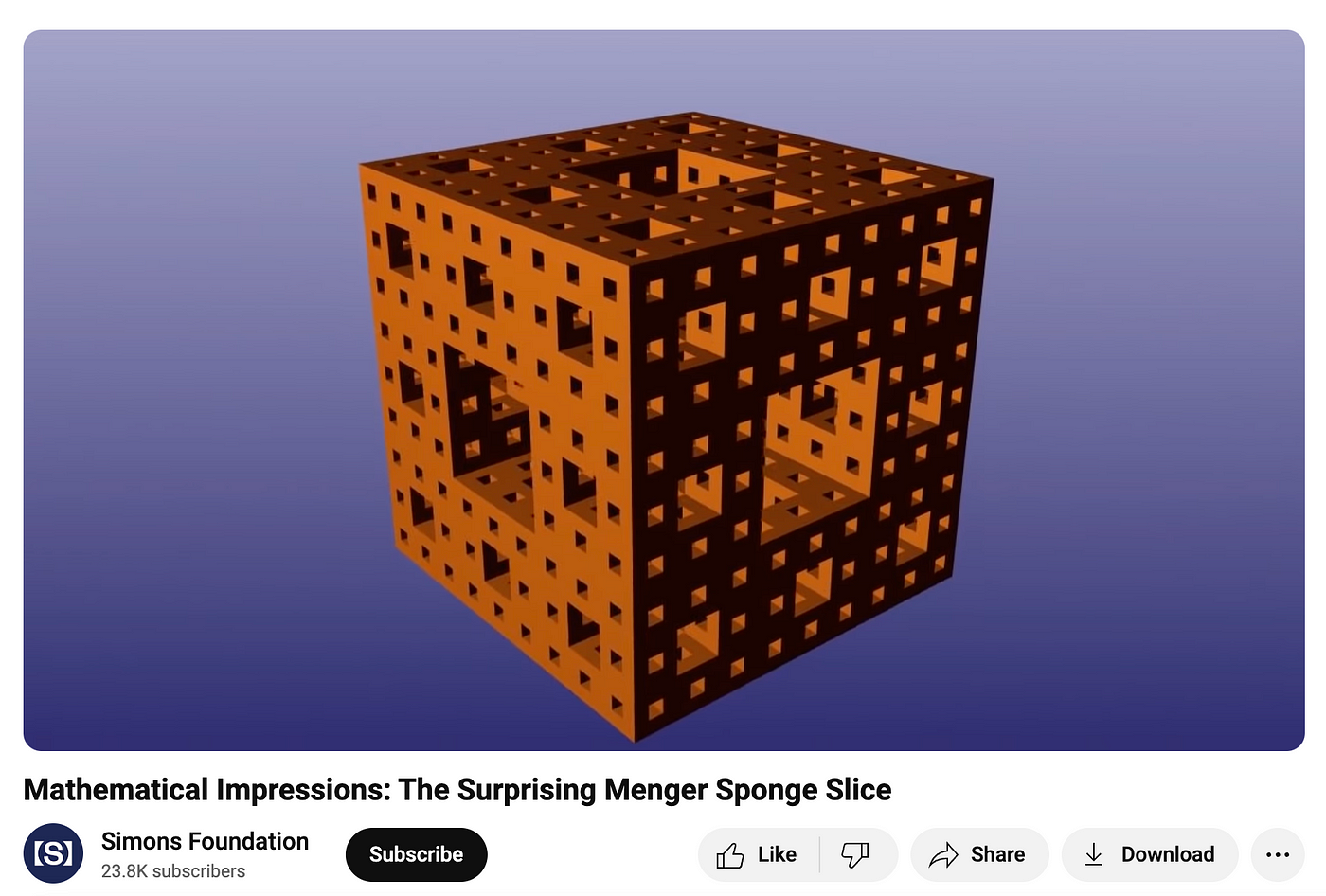
Essentially, “it is plain to see that this cube is in the end infinitely hollow. Its total volume approaches zero, while the total lateral surface of the hollowings infinitely grows” (ATP, 487).
In this Youtube video by the Simons Foundation, the narrator states:
As you [continue the process of hollowing out squares] infinitely many times, there is zero volume remaining, but infinite area — it’s all surface. (0:45–0:52)
Fractals such as the Van Koch Curve or the Sierpinski Sponge exemplify instances of smooth space that resist striation; they defy attempts at organizational structuring.
And now … the moment you’ve all been waiting for …
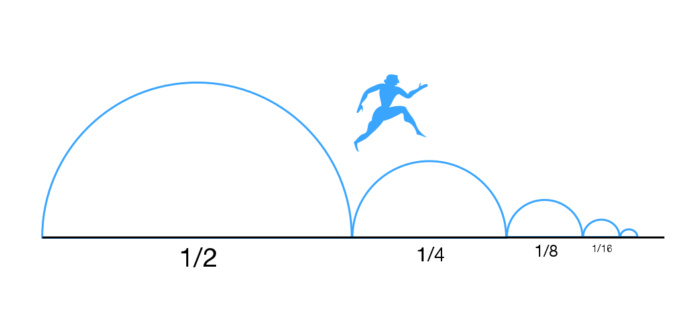
The problem with Zeno’s Paradox lies in its assumption that space/time is entirely striated.
Deleuze and Guattari state:
Achilles’ running is not divided into steps, his steps do not compose it in the manner of magnitudes. (ATP, 483)
To understand this point, we must draw from Bergson’s argument regarding duration. Achilles’ running is not divided into concrete steps, and each step does not compose the overall activity of running in the way that magnitudes accumulate. Essentially, like that of temperature, music, or distance, running is not composed of addable or displaceable magnitudes. Running operates like that of a continuous flow of duration. We must emphasize the qualitative and continuous nature of the experience of running, which is in contrast to a more metric or quantitative understanding that would break it down into discrete parts.
Therefore, Achilles’ running cannot be divided without changing in nature each time — just like the distance he traverses.
— —
Citation:
- Deleuze, Gilles and Guattari, Félix. A Thousand Plateaus. 1980. University of Minnesota Press. English Translation, 1987.
Leave a Reply